(ab bc ca)^2 572279-Ab+bc+ca 2ad

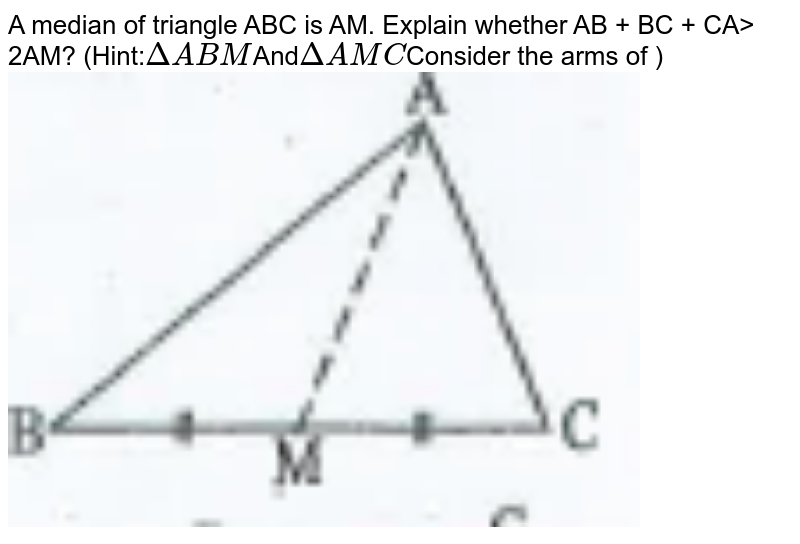
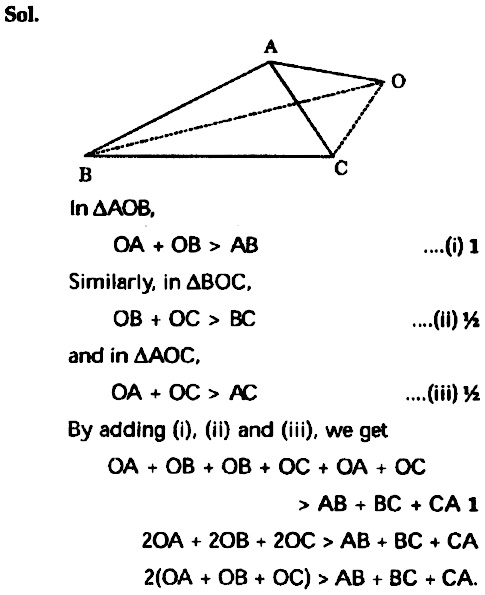
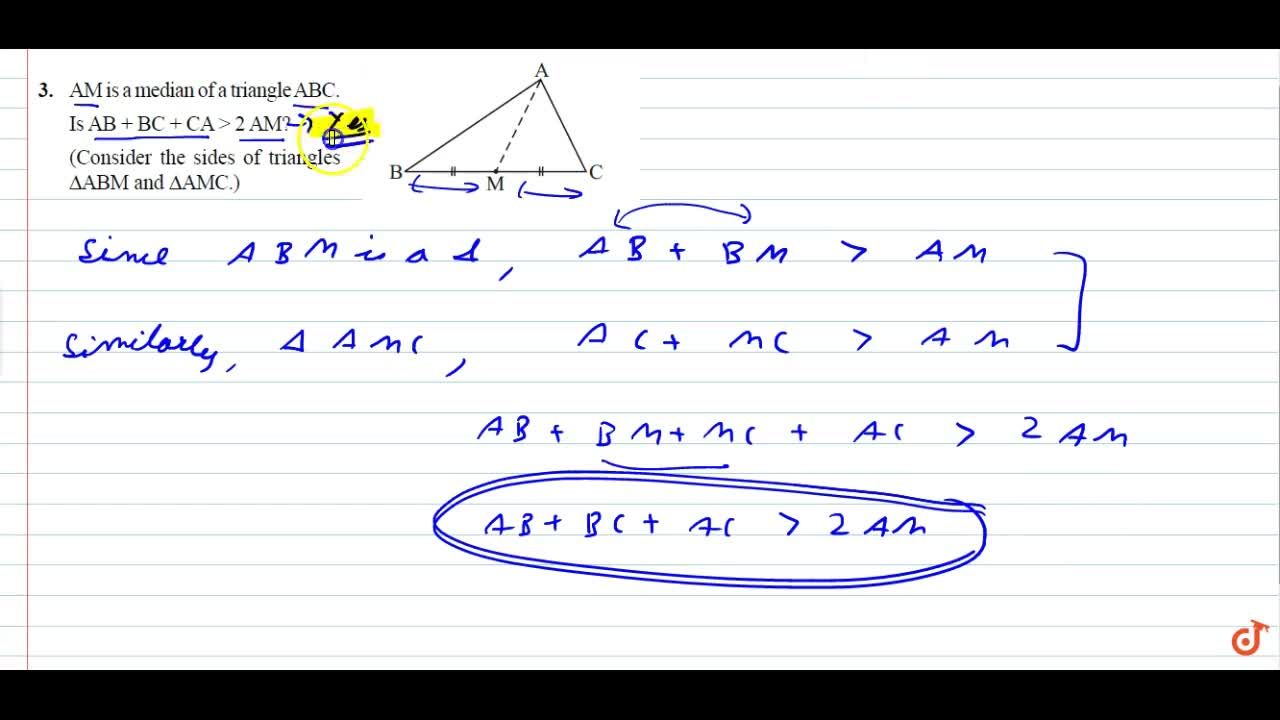
Q 3 Am Is A Median Of A Triangle Trustudies

Abc=1 => (abc)^2=1 a^2b^2c^22ab2bc2ca=1 => a^2b^2c^2abbcac3* (abbcac)=1 => a^2b^2c^2abbcac=0 => (ab)^2 (bc)^2 (ca)^2=0 Hence it follows, that a=b=c 35K views View upvotes Vivek Singh , Software Engineer at Tekion Answered 5 years ago Author has 236 answers and 6071K answer views It is very easy problemC ≤ ≤ ab=> cc ≤ ≤ c (ab) => c2 c 2 ≤ ≤ acbc (3) cộng vế với vế của (1);

Ab+bc+ca 2ad

Ab+bc+ca 2ad-NCERT Solutions NCERT Solutions For Class 12 NCERT Solutions For Class 12 PhysicsA 2 b 2 c 2 ab bc ca 2 2 Câu 229 Chọn D Câu230 AM BN AC CM BD DN AC BD CM DN 2 2 2 2 9 CM DN 2 2 2 Lại có CM MN

Ab Ca Does Not Exceed Cc

Share It On Facebook Twitter Email 1 Answer 1 vote Ex 42, 7 By using properties of determinants, show that 8(−a2&ab&ac@ba&−b2&bc@ca&cb&−c2) = 4a2b2c2 Solving LHS 8(−a2&ab&ac@ba&−b2&bc@ca&cb&−c2) Taking a common from R1, b common from R2 , c common from R3 = abc 8(−a&b&c@a&−b&c@a&b&−c) Taking a common from C1, b common Using properties of determinants, prove that (a^2,ab,ac)(bc,b^2,bc)(ca,cb,c^2) = 4a^2b^2c^2 asked in Mathematics by Aria (60k points) determinant;

 You can see that if you expand (abc)^2, simplify, multiply by 2, and use the trivial inequality Instead of doing AMGM, I managed to solve it using CauchySchwartz Inequality There is likely a solution with AMGM, but I don't see it So here is mine (a 3 b 3 c 3 ) (abbcca) ≥abc (abc) 2 Divide all by abcIf a b c = 4 and ab bc ca = 2, then a 3 b 3 c 3 – 3abc is equal to ∶ This question was previously asked in SSC CGL Previous Paper 57 (Held On 11 June 19 Shift 3) Download PDF Attempt Online View all SSC CGL Papers > 32;We have to subtract (2(abbcca)) from (abbcca)Now, the required answer is (=(abbcca)2(abbcca))(=abbcca2ab2bc2ca)(=3ab3bc3ca) Snapsolve

Ab+bc+ca 2adのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
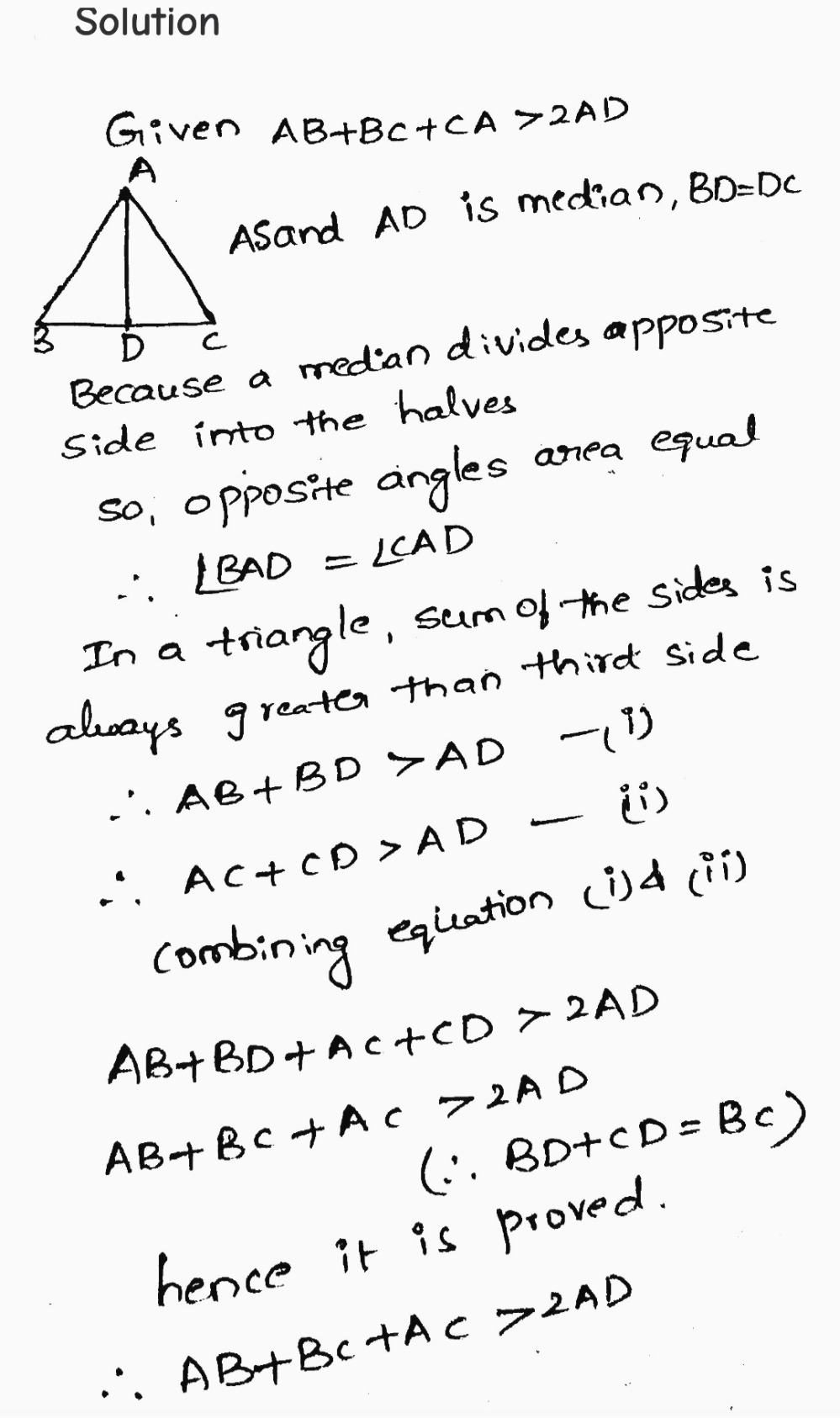Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	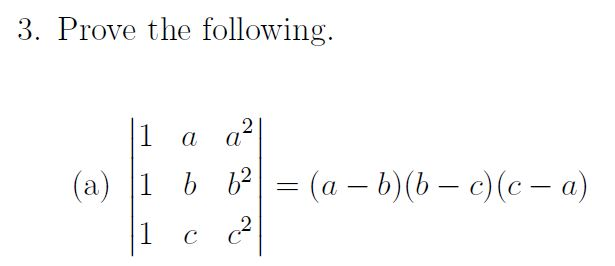Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	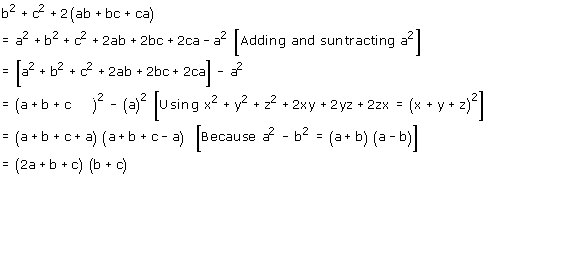Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	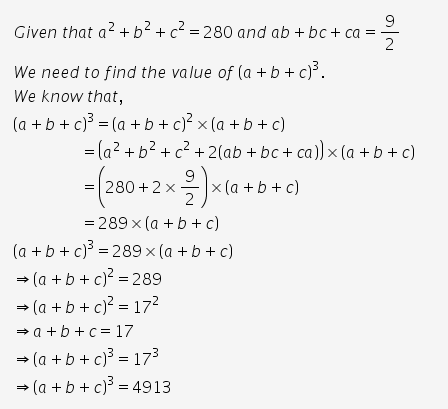Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	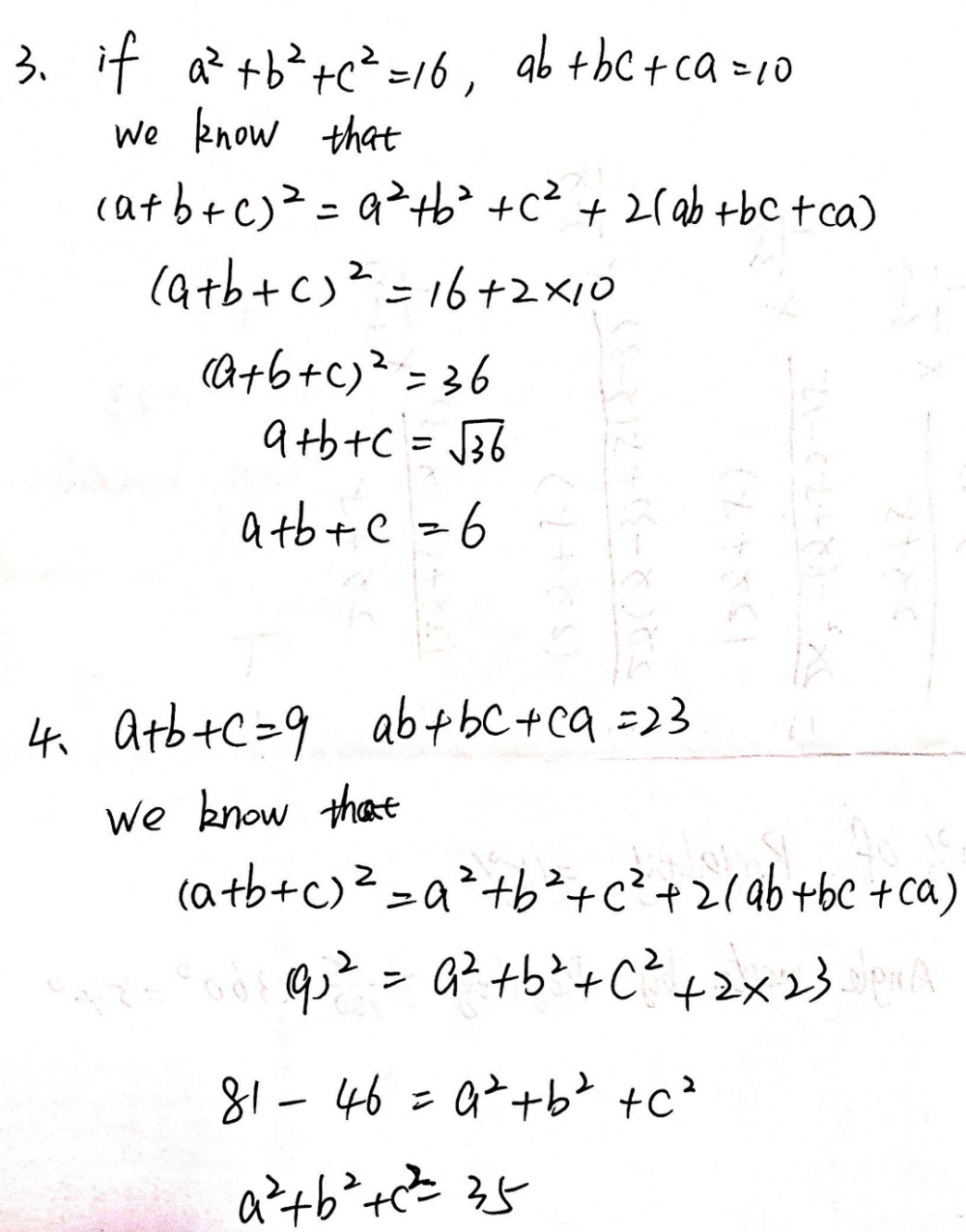Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	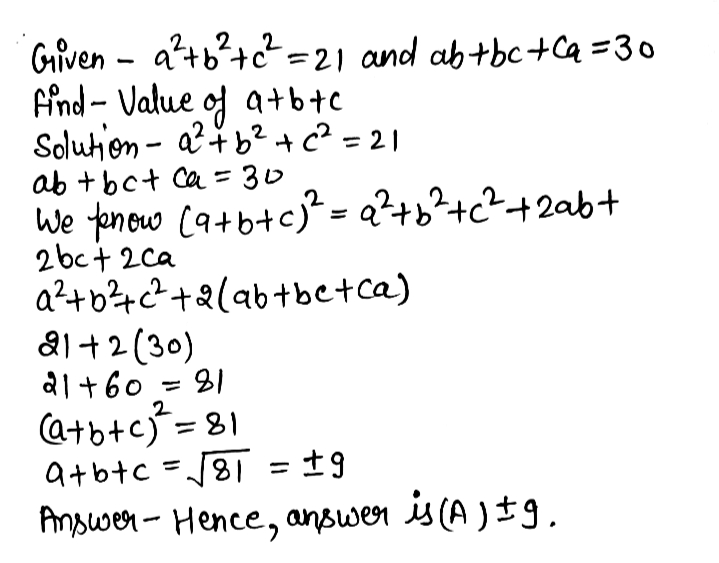Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	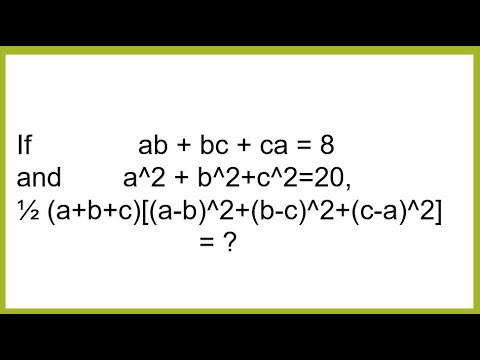Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving
Art Of Problem Solving	Art Of Problem Solving	Art Of Problem Solving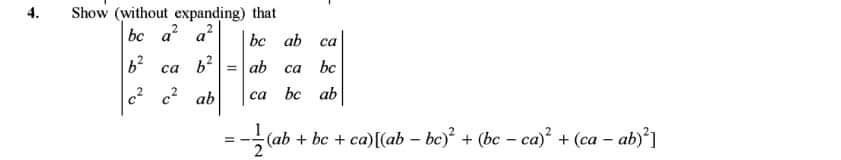
Art Of Problem Solving	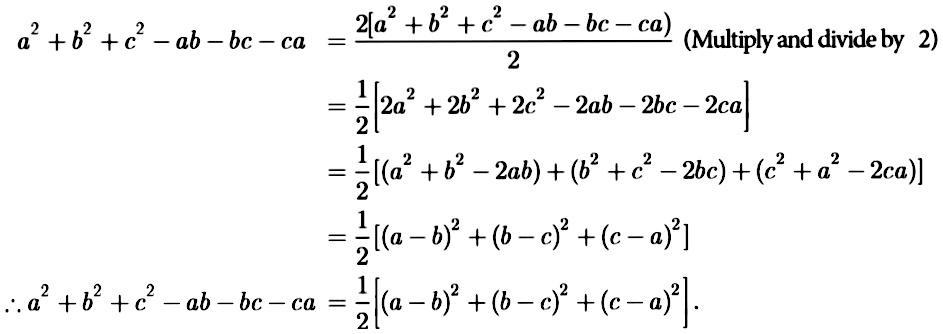Art Of Problem Solving

To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `b^2c^2,ab,ac , ba,c^2a^2,bc , ca,cb,a^2b^2`= a square of a determLet logx/(a^2abb^2)=log y/(b^2bcc^2)=log z/(c^2caa^2)=k so logx=k(a^2abb^2) log y=k(b^2bcc^2) log z=k(c^2caa^2) Now logx^(ab)*( a b c )^2 = a^2 b^2 c^a 2ab 2bc 2ca(a b c) 2 = a 2 b 2 c 2 2(ab bc ca) ⇒ (a b c) 2 = 258 2 × 113 ⇒ (a b c) 2 = 258 226 = 484 ⇒ (a b c) = √484 = 22

Incoming Term: (ab+bc+ca)^2, ab+bc+ca 2am, ab+bc+ca+2abc=1, (ab+bc+ca)^2 formula, ab+bc+ca 2ad, (ab+bc+ac)^2, ab=bc=26 ac=20, ab=bc=25 ac=40, ab=bc=20 ac=24, ab=bc=25 ac=14,